Reddit Interview Problems: The Game of Life

These days, I'm an engineering manager at Reddit, where I lead the Advertiser Optimization team. I was recently invited by the /r/RedditEng team to share an interview problem I previously used to screen candidates. It was published here, but I've reposted it here with better formatting.

I was introduced to technical interviews when I was applying to my first tech job back in 2012. I heard the prompt, scribbled my answer on the whiteboard, answered some questions, and left, black marker dust covering my hands and clothes. At the time, the process was completely opaque to me: all I could do was anxiously wait for a response, hoping that I had met whatever criteria the interviewer had.

These days, things are a little different. When I was an engineer it was me asking the questions and judging the answers. Now that I'm a manager, it's me who receives feedback from the interviewers and decides whether or not to extend an offer. I've had a chance to experience all sides of the process, and in this post I’d like to share some of that experience.

To that end, I'm going to break down a real question that we previously asked here at Reddit until it was retired, and then I'm going to tell you how it was evaluated and why I think it's a good question. I hope you'll come away feeling more informed about and prepared for the interview process.

The Game of Life

Suppose you have an M by N board of cells, where each cell is marked as "alive" or "dead." This arrangement of the board is called the "state," and our task is to compute the cells in the next board state according to a set of rules:

1. Neighbors: each cell has eight neighbors, up, down, left, right, and along the diagonals.
2. Underpopulation: a live cell with zero or one live neighbors becomes dead in the next state.
3. Survival: a live cell with exactly two or three live neighbors remains alive in the next state.
4. Overpopulation: a live cell with four or more live neighbors becomes dead in the next state.
5. Reproduction: a dead cell with exactly three neighbors becomes alive in the next state.

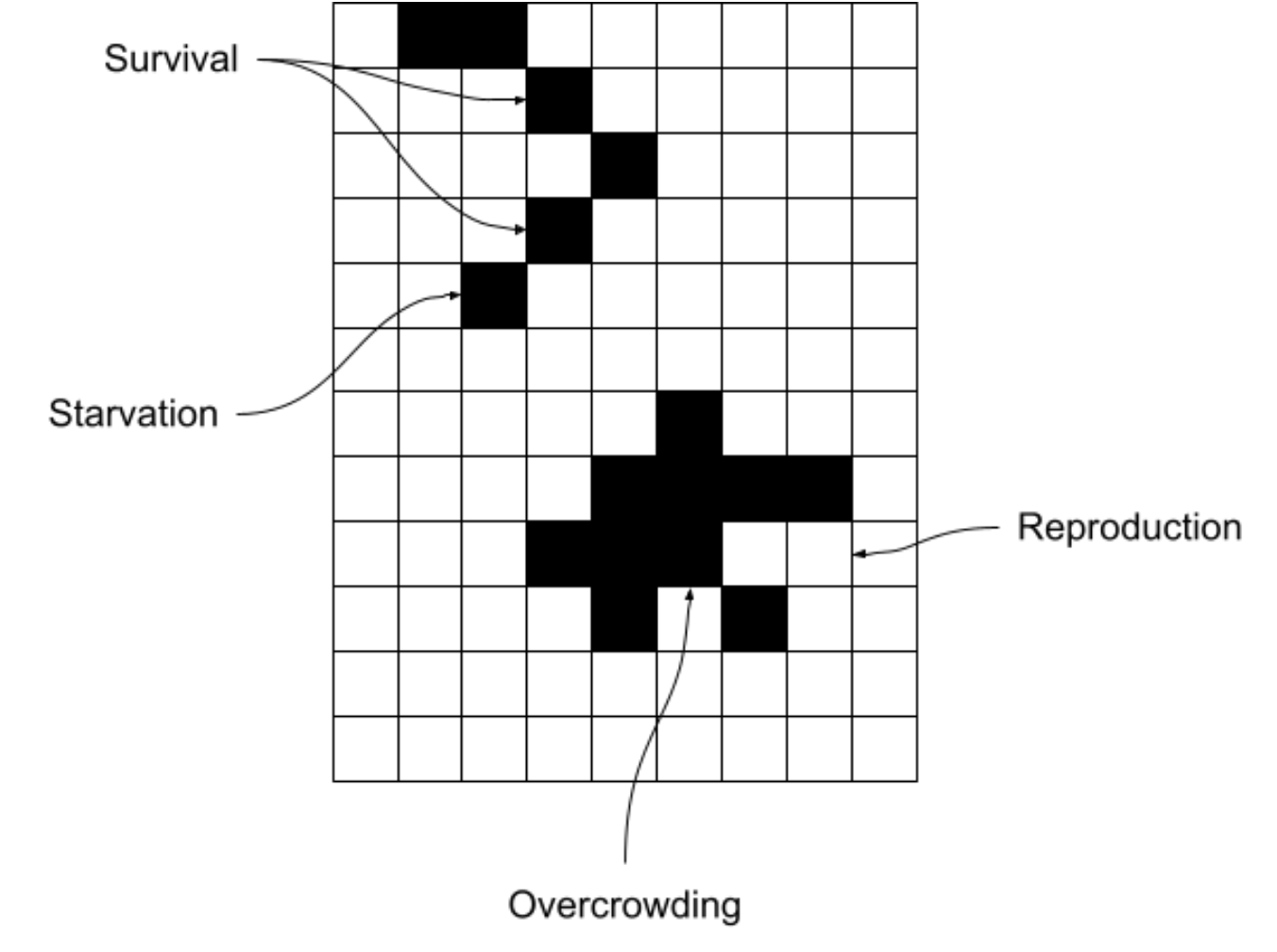
Things get interesting when you run this computation over and over again:

There's an entire branch of computer science dedicated to studying this device, but for now let's focus on implementing it.

Your task for the interview is: given an array of arrays representing the board state ( 'x' for alive and '' for "dead"), compute the next state.

I like this problem a lot. As we'll soon see, this problem is not quite as algorithmically difficult as some of the other problems I've written about in the past. Its complexity is mainly in the implementation, and I expect anyone with an understanding of arrays and basic control structure to be able to implement it. It’s a great interview problem for interns, and a somewhat easy interview problem for full-timers.

Solution: Part 1

Let's dive into that implementation complexity. We can decompose this problem into two parts: computing a new alive/dead status for an individual cell, and then using that per-cell computation to compute the next state for the entire board.

I say this in an offhand way, but being able to recognize and separate those two tasks is already an achievement. Some candidates rush in and attempt to solve both problems simultaneously, and while there's nothing wrong with that, it's much more difficult to do. Paradoxically enough, splitting the problem up is easier to implement, but is harder to do in practice because it requires a conceptual leap that comes with experience.

Anyway, the first part looks something like this:

LIVE_CELL = 'x'
DEAD_CELL = ' '

def update_cell(board, row, col):
    # Count the neighbors
    neighbor_count = 0

    for row_offset in (-1, 0, 1):
        for col_offset in (-1, 0, 1):
            if row_offset == 0 and col_offset == 0:
                continue

            new_row = row + row_offset
            if new_row < 0 or new_row >= len(board):
                continue

            # We assume here that every row has the same length, and that 
            # this condition is validated by the calling function.
            new_col = col + col_offset
            if new_col < 0 or new_col >= len(board[0]):
                continue

            if board[new_row][new_col] == LIVE_CELL:
                neighbor_count += 1
            elif board[new_row][new_col] != DEAD_CELL:
                raise ValueError('invalid cell value')

    if board[row][col] == LIVE_CELL:
            # Not overpopulation or underpopulation
            if not (neighbor_count <= 1 or neighbor_count >= 4):
                return LIVE_CELL
    elif neighbor_count == 3:
            # Reproduction
            return LIVE_CELL

    return DEAD_CELL

There are a few common mistakes that come up here:

• Not performing a bounds check when counting the neighbors and going off the edge of the board. This is prevented by checking that the evaluated row is greater than zero and strictly less than the size of the board.
• Mistakenly counting the target cell as a neighbor. We prevent this by skipping the cell when the row and column offsets are both equal to zero.
• Making logical errors when applying the logic. Getting this right comes with practice.

Solution Part 2: The Wrong Way

Now we need to actually call this method to perform the update. Here's where things get tricky. The naive solution is to just iterate over the cells on the board, decide whether they'll be alive or dead in the next state, and update immediately.

def update_state_wrong(board):
    for row in range(len(board)):
            for col in range(len(board[0])):
                board[row][col] = update_cell(board, row, col)

        return board

What's wrong with this, you might ask? The problem is that as you perform this update, your lookups into the board are mixing values that belong to the old board with values that belong to the new one. In fact, the values that belong to the new one actually destroy information: you don't know what the state of the old board was because you just overwrote it!  

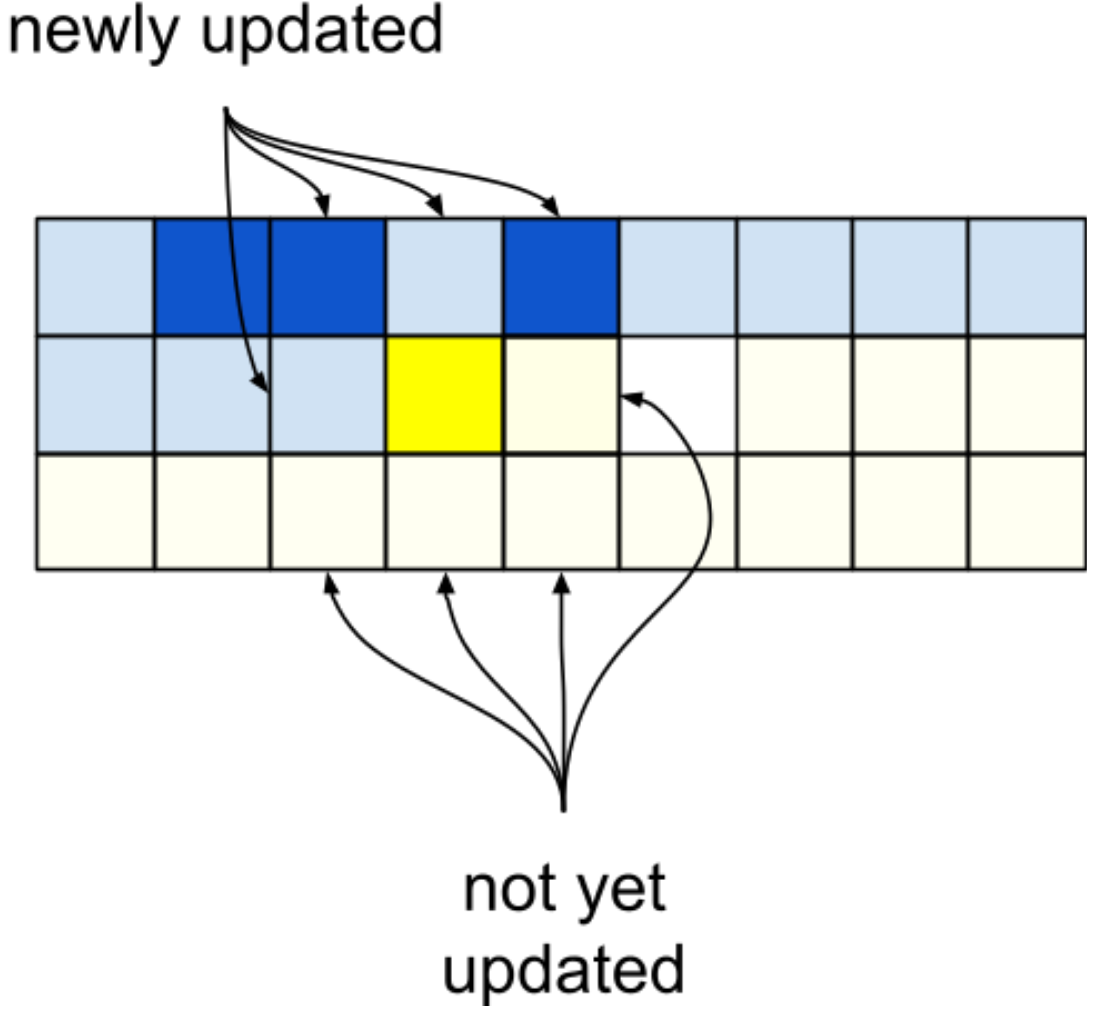
Solution Part 3: Correct but Wasteful

The easiest solution is also the simplest one: you make a copy of the old board, read from that one, and write to a new board. In python you can use the copy module to easily duplicate the board:

def update_state_slow(board):
    import copy
    old_board = copy.deepcopy(board)

    for row in range(len(board)):
            for col in range(len(board[0])):
                board[row][col] = update_cell(old_board, row, col)

        return board

This is a fine solution. It works, and it's correct. However, let's take a closer look at the access patterns to that old board over the course of this computation. Suppose we're computing the state of the cell marked with a star:

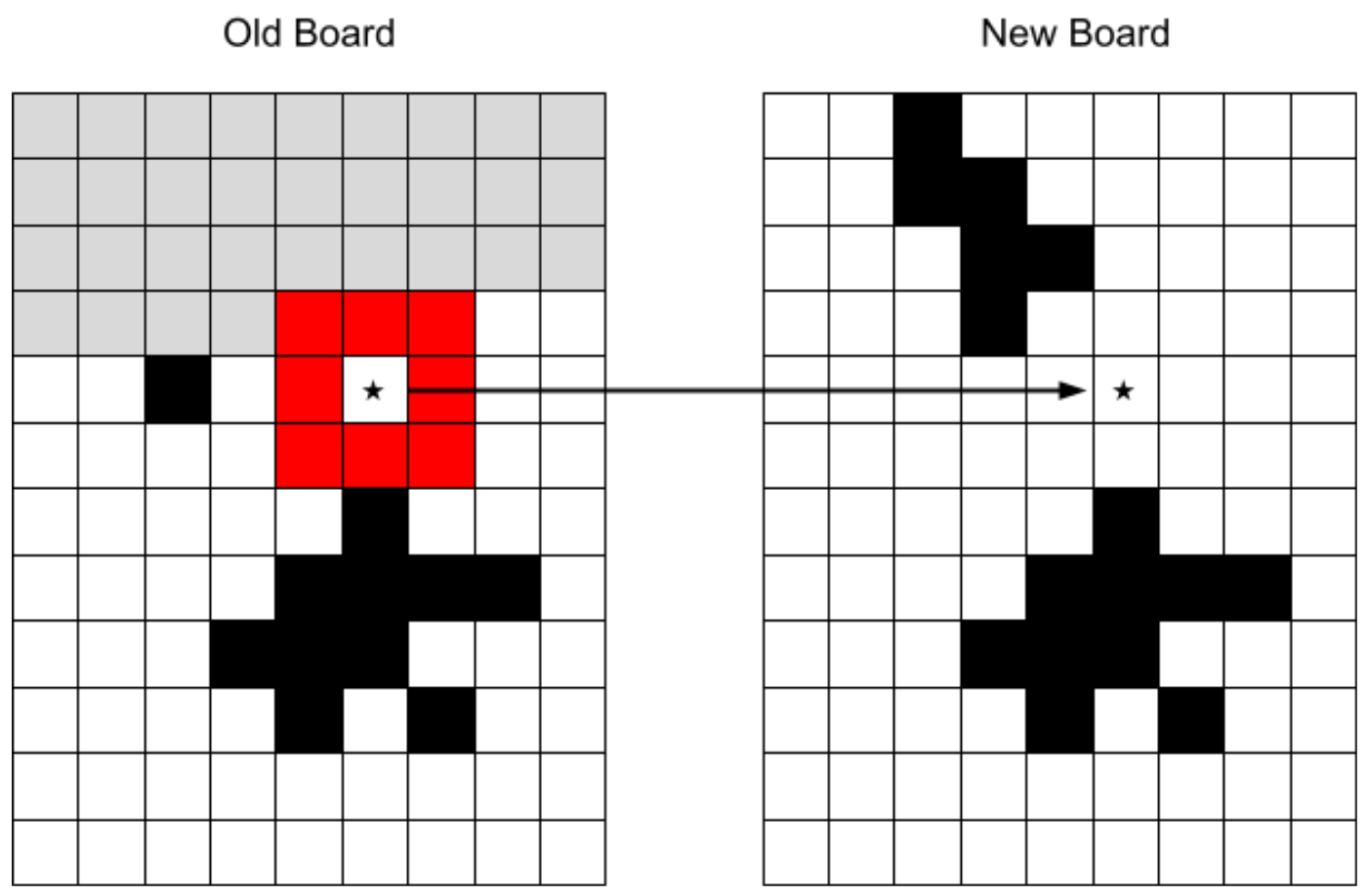
The only cells that are relevant to us are the ones surrounding it, marked in red. The cells marked in grey will never be read again. They are completely useless to the computation. The rest of the cells, the ones we haven't read yet, are duplicated between the old and new board. The vast majority of the memory we're using to store the old board is being wasted, either because it'll never be read or because it could be read from elsewhere.

This might not seem like a big deal, and honestly I wouldn't hold it against a candidate if they stopped at this solution. Getting this far during an interview setting is already a good sign. In reality, though, these sorts of suboptimal solutions matter. If your input is large enough, resource waste like this can cripple an otherwise correct and usable system. I give more points to candidates who point out this waste and at least describe how to address it.

Solution Part 4: Correct and (Mostly) Optimal

If you look carefully, the only data that we actually need to copy are the previous and the current rows: older rows will never be read from again, newer rows aren't needed yet. One way to implement this is to always read from the old board, and perform our writes to a temporary location, only changing cells on the board for rows that we're confident we'll never need to read again:

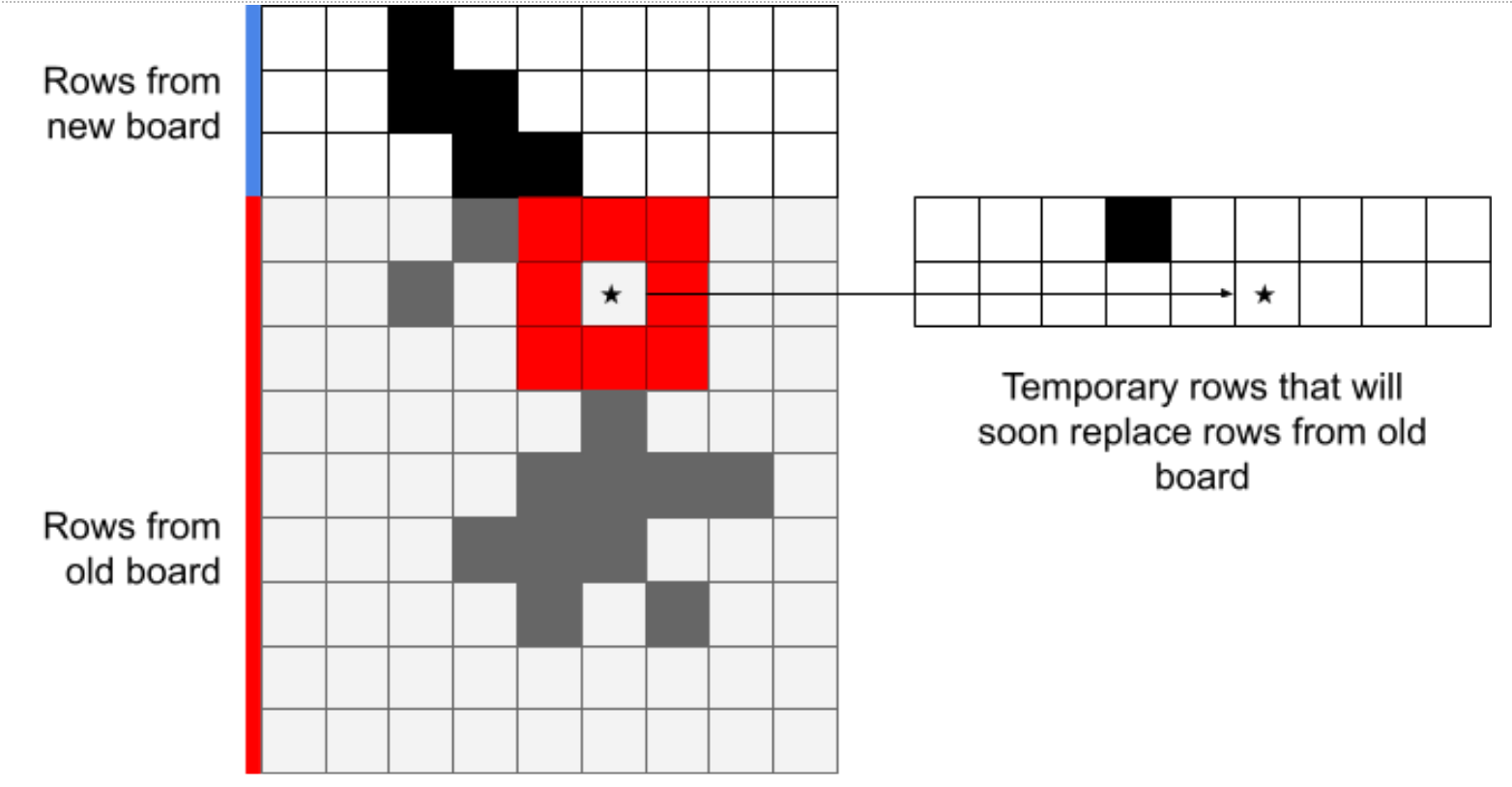
Here's an implementation of this approach:

def update_state_correct(board):
    # Maintain the previous row to be updated.
    previous_row = None

    for row in range(len(board)):
        current_row = []

        # Write our updates into the temporary row.
        for col in range(len(board[0])):
            current_row.append(update_cell(board, row, col))

        # If the previous row was updated, swap it into the board.
        if previous_row:
            board[row - 1] = previous_row

        # Record our writes for this row for writing and 
        # replacement in the next iteration.
        previous_row = current_row

    # Don't forget to update the last row! This is a very common mistake.
    if len(board) > 1:
            board[-1] = previous_row

    return board

This solution is pretty close to optimal: it only uses two rows worth of temporary data, instead of an entire board. Strictly speaking, it’s not quite optimal, because we’re storing data in the previous_row variable that we could be writing out during traversal. However, this solution is pretty close, and the full solution is rather complex, so I'll leave improving on this one as an exercise for the reader.

Bonus Part: Go Big or Go Home

We could stop here, but why should we? As another exercise for the reader, consider the problem of ridiculously large boards: instead of a few hundred cells, what if your board had trillions of cells? What if only a small percentage of those cells was populated at any given time? How would your solution change? A few follow ups come to mind:

• The implementations I presented here are dense, meaning they explicitly represent both live and dead cells. If the vast majority of the board is empty, representing dead cells is wasteful. How would you design a sparse implementation, i.e. one which only represents live cells?
• These inputs have edges, beyond which cells cannot be read or written. Can you design an implementation that has no edges and allows cells to be written arbitrarily far out?
• Suppose you were computing more live cells than could reasonably be represented on a single machine. How would you distribute the computation uniformly across nodes? Keep in mind that over multiple iterations dead cells that were nowhere near live ones can eventually become live as live cells "approach" the dead ones.

Discussion

So that's the problem! If you got as far as part 3 in a 45 minute interview at Reddit, I would usually give a "Strong Hire" rating for interns and a "Hire" for full-timers. Amusingly enough, I was given this question way back when as one of my interviews for a Google internship. I quickly implemented part 3, and I can’t remember whether I actually implemented part 4 or just described its advantages, but I ended up receiving an offer.

I like this problem because it's not as algorithmically difficult as some of the other problems out there. There's a healthy debate among both hiring managers and the broader engineering community about the level of difficulty that should be used in these interviews, and my (and Reddit's) use of questions like this represents a sort of implicit position on this debate.

The views go something like this: on one hand, tougher problems allow you to filter out all but the very best candidates, resulting in a stronger engineering team. If a candidate can solve a difficult problem under pressure, they likely have the knowledge and intuition to solve the kinds of problems the company will require. It’s a sort of “if you can make it here, you can make it anywhere” philosophy.

On the other hand, harder problems risk over-emphasizing algorithmic skills at the expense of measuring craftsmanship, soft skills, and more hard-to-measure engineering intuition. It also risks shutting out people from nontraditional backgrounds by asking questions that are de-facto tests of academic knowledge.

I believe questions like this one represent a happy medium between these two: they're easy to understand but hard to get right, and instead of an algorithmic flash of insight, they require strong implementation and optimization skills. Also, hiring panels often include multiple questions, each targeting a different skill. Any single interview isn't enough to justify an offer, but a slate of "hire" or "strong hire" feedback suggests a candidate has a breadth of experience and should be considered for an offer.

Conclusion

I hope you found this writeup helpful and educational! You can support this blog by becoming a patron. Make sure to checkout /r/RedditEng for more posts by my colleagues at Reddit. Also, if you're looking for a job and would like to work at Reddit, we're hiring! You can find all our job postings on our careers page.