Google Interview Problems: Ratio Finder

Welcome to yet another installment of my series on interview questions I used to ask at Google before they were leaked and banned. I’ve since left being a software engineer at Google and moved on to being an engineering manager at Reddit, but I’ve still got a few great questions to share. So far I’ve covered dynamic programming, matrix exponentiation, and query synonymity, and this time around I’ve got a brand new question for us to dig into.

Before we begin, two notes. First off, working at Reddit has been amazing, and I’ve spent the past eight months building and leading the new Ads Relevance team and setting up the new engineering office in New York. As much fun as that has been, I’ve unfortunately found it hasn’t left me much time or energy to write until recently, and so I’m afraid this series has become a little neglected. Sorry for the delay.

Secondly, if you’ve been keeping up with this series you might have come away from my last post with the expectation that I’ll dig into variants of query synonymity. While I would like to do this at some point, I must confess this job change has caused me to lose momentum on that problem, and I’ve decided to shelve it for now. Stay tuned, though! I owe you all a writeup, and I intend to deliver it to you. Just, you know, later…

Quick disclaimer: while interviewing candidates is one of my professional responsibilities, this blog represents my personal observations, my personal anecdotes, and my personal opinions. Please don’t mistake this for any sort of official statement by or about Google, Alphabet, Reddit, or any other person or organization.

Join our discord to discuss these problems with me and the community!

Finding a New Question

In my last post I described one of my favorite questions, one which I used for a long time before it was inevitably leaked and banned. Previous questions I had used were fascinating from a theoretical standpoint, but I wanted to pick a problem that was a little more relevant to Google as a company. When that question was banned I wanted its replacement to satisfy a new constraint: I wanted it to be easier.

Now it might seem a little surprising to hear this, given how notoriously difficult the Google interview process is. However, at the time an easier problem made perfect sense. My reasoning had two parts. The first part was pragmatic: candidates tended not to do well on my previous questions despite multiple hints and simplifications, and I wasn’t always entirely sure why. The second part was theoretical: the interview process should separate candidates into categories of “worth hiring” and “not worth hiring,” and I was curious as to whether a slightly easier question would still allow me to do this.

Now before I elaborate on what these two things mean, I’m going to point out what they don’t mean. “I’m not always sure why this person is struggling” does not mean I thought hard questions weren’t useful and that I wanted to make the interview process easier. Even the hardest question had plenty of candidates who performed well on it. What it means is that when candidates struggled, I had a difficult time constructing a narrative around where they are lacking.

Good interviews provide a broad picture of a candidate’s strengths and weaknesses. Simply saying “they rocked” doesn’t do much to help the hiring committee decide whether the candidate has the company-specific characteristics they’re looking for. Similarly, simply saying “they bombed” doesn’t help the committee when they have a candidate who is strong in some areas but might deserve the benefit of the doubt in others. I found more difficult questions caused candidates to fall into one of these two buckets more often than I would have liked. In this light, “I’m not always sure why they were struggling” means “failure to progress on this question doesn’t by itself paint a picture of this candidate’s abilities.”

“Classifying candidates into ‘worth hiring’ and ‘not worth hiring’” does not mean “the interview process should separate dumb candidates from the smart ones.” I can’t remember any candidates I spoke to who weren’t intelligent, talented, and motivated. Many of them came from excellent schools, and the ones who didn’t were clearly exceptionally self motivated. Simply making it past a phone screen is a good sign, and even rejection at that stage is no indication of lack of ability.

However, I can remember many who were not sufficiently prepared for the interview, or worked at too slow a pace, or required too much supervision to solve a problem, or communicated in an unclear way, or failed to translate their ideas into code, or had an attitude that simply wasn’t going to lead them to success in the long term, etc. The definition of “worth hiring” is squishy and varies by company, and the interview process is there to see how well each candidate fits into a given company’s definition.

After reading many reddit comments sections complaining about how they thought interview questions were unnecessarily difficult, I was curious to see if I could still make a “worth it/not worth it” recommendation using an easier problem. My suspicion was that it would give me useful signal while simultaneously making things easier on the candidate’s nerves. I’ll discuss my findings at the end of this post…

All these concerns were top of mind as I was choosing a new question. In a perfect world, I would use one that wasn’t so difficult that it couldn’t be solved in 45 minutes, but at the same time could be elaborated a bit to let stronger candidates show their skills. It would also need to be compact in its implementation, because even though text editor-only chromebooks were beginning to enter the interviewing room at this time, a lot of candidates still used the whiteboard. It was also a major bonus if it was somehow related to Google’s products.

I finally settled on a question some wonderful Googler had carefully written up and inserted into our question database. I’ve reached out to someone I know at Google to confirm that it is still banned, so you shouldn’t expect to see it during your interviews. I’m presenting it in a way that I found effective, with apologies to the original author.

The Question

Let’s talk about measuring distance. A hand is a unit of distance equal to four inches, and is commonly used to measure the height of horses in English-speaking countries. A light year is another unit of distance equal to the distance a particle (or is it wave?) of light travels in a certain number of seconds, equal roughly to one Earth year. On the face of it, these two units have little to do with one another beyond being used to measure distance, but it turns out that Google can convert between them pretty easily:

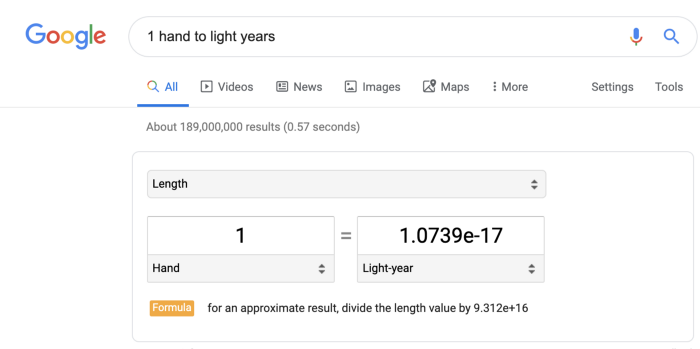
This might seem obvious: after all, they both measure distance, so of course there’s a conversion. But when you think about it, it’s a little odd: how did they compute this conversion rate? Surely no one actually counted the number of hands in a light year?

Of course not. It turns out you don’t actually need to count this directly. You can just use commonly-known conversions:

• 1 hand equals 4 inches
• 4 inches equals 0.33333 feet
• 0.33333 feet equals 6.3125e-5 miles
• 6.3125e-5 miles equals 1.0737e-17 light years

The aim of this problem is to design a system that will perform this conversion for us. To be precise:

Given a list of conversion rates (formatted in the language of your choice) as a collection of origin unit, destination unit, and multiplier, for example:

foot inch 12

foot yard 0.3333333

...etc., such that ORIGIN * MULTIPLIER = DESTINATION, design an algorithm that takes two arbitrary unit values and returns the conversion rate between them.

Discussion

I like this problem because it has a pretty intuitively obvious answer: just convert from one rate to another and then to another until you find the goal! I can’t recall a single candidate who encountered this problem and was completely mystified as to how they would solve it by hand. This boded well for my “easier” requirement, since other questions tend to required long minutes of staring and meditating before the candidate arrived at even a basic approach.

And yet, I’ve seen plenty of candidates who weren’t able to drive this intuition to a working solution without significant hints. One of the strengths of this question is that it tests the candidate’s ability to frame a problem in a way that yields to both analysis and coding. As we will see, it also features a very interesting extension that requires yet another conceptual leap.

For context, framing is the act of translating a problem where the solution is not obvious into an equivalent one where the solution yields naturally. If that sounds completely abstract and unapproachable, forgive me because it is. I’ll explain what I mean as I provide the initial solution to this problem. The first part of this solution will be an exercise in framing and application of algorithmic knowledge. The second part will be an exercise in manipulating that knowledge to arrive at a novel and non-obvious optimization.

Part 0: The Intuition

Before we dig deeper, let’s fully investigate the “obvious” solution. Most of the conversions we are asked to perform are simple and straightforward. Any American who’s traveled outside the United States knows that most of the world uses a mysterious unit called a “kilometer” to measure distance. Converting from one to another is as simple as multiplying miles by roughly 1.6.

This is about the depth of complexity that we will encounter for most of our lives. For most units, there’s already a precomputed conversion, and all we need to do is look it up in the appropriate chart. However, for the tougher ones for which we have no direct conversion (such as hands to light years), it’s not unreasonable to plot out a conversion path (duplicated from above):

• 1 hand equals 4 inches
• 4 inches equals 0.33333 feet
• 0.33333 feet equals 6.3125e-5 miles
• 6.3125e-5 miles equals 1.0737e-17 light years

That wasn’t hard at all, I just came up with that conversion using my imagination and a standard conversion chart! Some questions remain, though. Is there a shorter way to do this conversion? How accurate is this rate? Is there always a conversion? Can we automate it? Unfortunately, here is where our naive approach breaks down.

Part 1: The Naive Solution

As nice as it is that this problem has an intuitive solution, that approachability is actually an obstacle to solving this problem. There is nothing harder than learning something you already know, not least because you often don’t know nearly as much about it as you think you do. To illustrate, imagine you’re in an interview room and you’ve got this approach in your head. There’s a number of crucial concerns that the intuitive approach does not enable you to address.

For instance, what if there is no conversion? The obvious approach doesn’t tell you anything about whether there actually is a conversion, and if I were given a thousand conversion rates, I would have a very difficult time determining whether such a conversion exists. Perhaps I’m being asked to convert between unfamiliar (or made up) units called wobbles and a thingles, and I have no idea where to even start. How would the intuitive approach handle that?

I have to admit, that’s kind of a contrived scenario, but there’s another, more realistic one to consider. You’ll notice that my problem statement only includes units of distance. This is very intentional. What if I ask my system to translate from inches to kilogram? You and I both know this can’t be done because those units measure different things, but our input tells us nothing about the “kind” of thing each unit measures.

This is where the careful statement of the question allows strong candidates to shine. Strong candidates think through the edge cases of a system before they design an algorithm, and this problem statement purposefully gives them an opportunity to ask me whether we’ll be translating different units. It’s not a huge deal if they don’t catch this issue early on, but it’s always a good sign when someone asks me “what should I return if there is no conversion?” Stating the question this way gives me an indication of the candidate’s abilities before they write a single line of code.

The Graph Framing

Clearly the naive approach isn’t going to be helpful, so we have to ask ourselves, how can we translate this? The answer is the first leap of insight required by this problem: treat the units as a graph.

In particular, imagine each unit is a node in a graph, and there exists an edge from node A to node B if A can be converted into B:

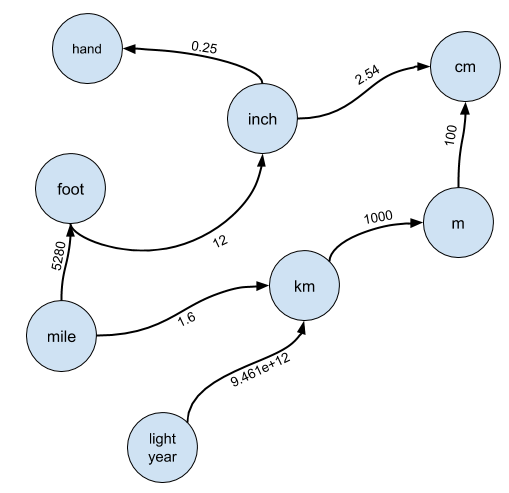
The edges are labeled with the conversion rate you must multiply A by to arrive at B.

I almost always expected the candidate to come up with this framing, and I rarely gave major hints toward it. I can forgive a candidate not noticing a problem can be solved using disjoint sets, or not knowing enough linear algebra to realize a problem reduces to repeated exponentiation of the adjacency matrix, but every CS program and bootcamp worth its salt teaches graphs. If a candidate doesn’t have the CS skills to know a graph problem when they see one, that’s a “not worth hiring” signal.

Anyway

Framing the problem as a graph unlocks all the classic graph search problems. In particular, two algorithms are useful here: breadth first search (BFS) and depth first search (DFS). In breadth-first search, we explore nodes according to their distance from the origin:

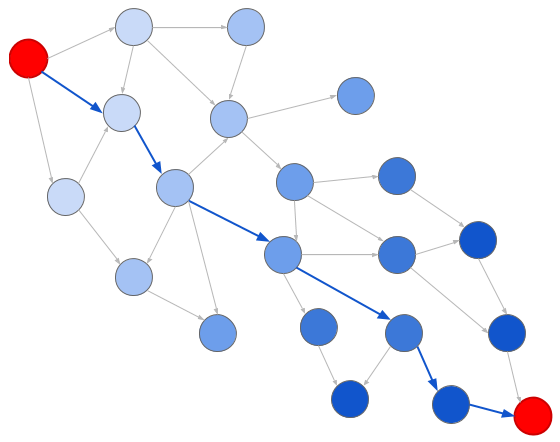
Whereas with depth-first search, we explore nodes in the order in which we encounter them:

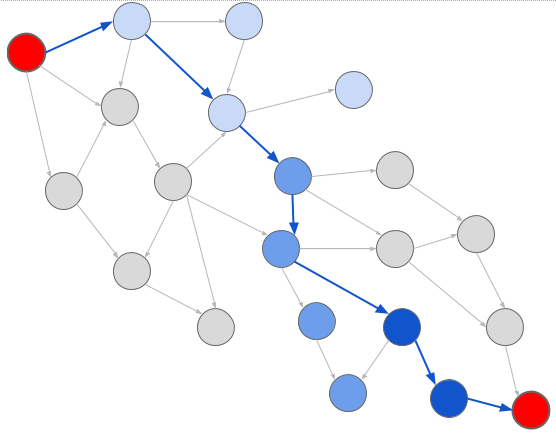
Using either of these, we can easily determine whether there exists a conversion from one unit to another simply by performing a search over the graph. We start at the origin unit and search until we find the destination unit. If we fail to find the destination (as when trying to convert inches to kilograms), we know there is no path.

But hang on, something is missing. We don’t want to find whether a path exists, we want to find the conversion rate! This is where the candidate must make a leap: it turns out you can modify any search algorithm to find the conversion rate, simply by keeping additional state as you traverse. Here’s where the illustrations stop making sense, so let’s dive right in to some code.

First off, we need to define a graph data structure, so we’ll use this:

class RateGraph(object):
    def __init__(self, rates):
        'Initialize the graph from an iterable of (start, end, rate) tuples.'
        self.graph = {}
        for orig, dest, rate in rates:
            self.add_conversion(orig, dest, rate)

    
    def add_conversion(self, orig, dest, rate):
        'Insert a conversion into the graph.'
        if orig not in self.graph:
            self.graph[orig] = {}
        self.graph[orig][dest] = rate


    def get_neighbors(self, node):
        'Returns an iterable of the nodes neighboring the given node.'
        if node not in self.graph:
            return None
        return self.graph[node].items()
        

    def get_nodes(self):
        'Returns an iterable of all the nodes in the graph.'
        return self.graph.keys()

Next, we’ll get to work on DFS. There are many ways of implementing DFS, but by far the most common one I’ve seen is the recursive solution. Let’s start with that:

from collections import deque

def __dfs_helper(rate_graph, node, end, rate_from_origin, visited):
    if node == end:
        return rate_from_origin

    visited.add(node)

    for unit, rate in rate_graph.get_neighbors(node):
        if unit not in visited:
            rate = __dfs_helper(rate_graph, unit, end, rate_from_origin * rate, visited)
            if rate is not None:
                return rate

    return None

def dfs(rate_graph, node, end):
    return __dfs_helper(rate_graph, node, end, 1.0, set())

In a nutshell, this algorithm starts with a node, starts iterating over its neighbors, and immediately visits each by performing a recursive function call. Each function call in the stack stores the state of its own iteration, so when one recursive visitation returns, its parent immediately continues iterating. We avoid visiting the same node twice by maintaining a visited set across all invocations. We also compute the rate by assigning to each node the conversion rate between it and the origin. This way, when we encounter the destination node/unit, we’ve already built up the conversion rate from the origin, and we can simply return it.

This is a fine implementation, but it suffers from two major weaknesses. First off, it is recursive. If it turns out the path we need is more than a thousand or so hops long, we’ll crash. Sure, it’s not likely, but if there’s one thing you don’t want happening in a long-running service, it’s crashing. Second off, even if we were to stop successfully, our answer has some undesirable properties.

I actually already gave you a hint way up at the top of the post. Did you notice how Google says the conversion rate is 1.0739e-17 but the conversion I computed manually came out to 1.0737e-17? It turns out given all the floating point multiplications we’re performing, we have to start worrying about error propagation. The subtleties are a little more than I want to go into for this post, but the gist of it is we want to perform as few floating point multiplications as possible to avoid errors accumulating and causing trouble.

DFS is a fine search algorithm, and if a solution exists it will find it, but it lacks a crucial property: it does not necessarily find the shortest path. This is relevant to us because a shorter path means fewer hops, which means fewer error-propagating floating point multiplications. To get around this, we’ll want to use BFS.

Part 2: The BFS Solution

At this point, if a candidate has successfully implemented a recursive DFS solution and stopped there, I would usually give them at least a weak hire recommendation. They understood the problem, chose an appropriate framing, and implemented a working solution. It’s a naive solution, so I’m not exactly jumping to hire this person, but if they performed well on their other interviews then I’m not going to recommend a rejection.

This bears repeating: when in doubt, write out a naive solution! Even if it’s not fully optimal, having code on the board is an accomplishment, and you can often iterate on it to get to a proper solution. Another way of saying this is: never let work go to waste. Odds are you thought of a naive solution but didn’t want to throw it out there because you know it’s not optimal. If you have a better solution on the tip of your tongue, that’s fine, but if not make sure you bank the progress you’ve made before you move on to more sophisticated things.

From here on out, we’re talking improvements, and the recursive DFS solution’s major weaknesses are that it’s recursive and it doesn’t minimize the number of multiplications. BFS,as we’ll soon see, does minimize the number of multiplications, and it also happens to be very tricky to implement recursively. Unfortunately we’ll have to scrap the recursive DFA solution, as improving on it will require a complete rewrite.

Without further ado, I present an iterative BFS-based approach:

from collections import deque

def bfs(rate_graph, start, end):
    to_visit = deque()
    to_visit.appendleft( (start, 1.0) )
    visited = set()

    while to_visit:
        node, rate_from_origin = to_visit.pop()
        if node == end:
            return rate_from_origin
        visited.add(node)
        for unit, rate in rate_graph.get_neighbors(node):
            if unit not in visited:
                to_visit.appendleft((unit, rate_from_origin * rate))

    return None

This implementation is functionally very different from the earlier one, but if you looks carefully you’ll notice it does roughly the same thing, with one major change. The biggest change is that while recursive DFS stores the state of what to visit next in the call stack, effectively implementing a LIFO stack, the iterative solution stores it in a FIFO queue.

This is the source of the “shortest path/fewest multiplications” property. We visit nodes in the order in which they are encountered, and so get generations of nodes. The first node inserts its neighbors, and then we visit those neighbors in order, all the while attaching their neighbors, and so on. The source of the shortest path property is that nodes are visited in order of their distance from the origin, so when we encounter the destination, we know there is no earlier generation that could have led to it.

At this point, we’re almost there. There are a few questions we need to answer first, and they both involve coming back to the original problem statement.

First, and most trivially, what if the input unit does not exist? That’s easy, nodes and units are equivalent, so if we can’t find a node with the given name then the unit doesn’t exist. In practice we need to perform a fair bit of string normalization so that “Pound” and “lb” and “POUND” all map to “pound” (or some other canonical representation), but that’s beyond the scope of this question.

Second, what if there is no conversion between two units? Recall that our input only gives us conversions between units, and it gives no indication of whether two units can be converted from one to another. This solution solves for this: conversions and paths are directly equivalent, so if there’s no path from one to another then there’s no conversion. In practice what happens is you end up with disconnected islands of units, one for distances, one for weights, one for currencies, etc.

Finally, if you look carefully at the graph I gave you at the top, it turns out you can’t actually convert between hands and light years using this solution:

Unfortunately, as the conversions were stated, the directed edges mean there is no path from hand to light-year. This is fairly easy to fix, though, since the conversions can be reversed by taking the reciprocal of the rate. We can modify our graph initialization code as follows:

def add_conversion(self, orig, dest, rate):
    'Insert a conversion into the graph. Note we insert its inverse also.'
    if orig not in self.graph:
        self.graph[orig] = {}
    self.graph[orig][dest] = rate

    if dest not in self.graph:
        self.graph[dest] = {}
    self.graph[dest][orig] = 1.0 / rate

Part 3: Evaluation

That’s it! If a candidate got to this point, I would strongly consider giving them a firm “Hire” recommendation. If you studied computer science or took an algorithms course, you might be saying to yourself “is that really all it takes to pass this guy’s interview?”, to which my answer is “yeah, pretty much.”

Before you think this question is easy, though, let’s consider what a candidate has to do to arrive at this point:

• Understand the question
• Frame the conversion network as a graph
• Realize conversion rates can be mapped to paths through the graph
• Recognize they can use search algorithms to accomplish this
• Choose their favorite algorithm and modify it to track the conversion rate
• If they implemented DFS as a naive solution, realize its weaknesses
• Implement BFS
• Step back and examine the edge cases:
• What if we’re asked for a nonexistent node?
• What if the conversion rate does not exist?
• Realize the reversing the conversions is possible and likely necessary

This question is easier than the others I’ve asked and at the same time just as hard. As with all my previous questions, it requires that the candidate make a mental leap from an abstractly stated question to an algorithm or data structure framing that unlocks progress. The only thing that’s easier is that the algorithm to which they need to leap is less advanced than what other questions required. Outside this algorithmic stuff, the same demands are in place, especially around edge cases and correctness.

“But wait!”, you might ask, “Doesn’t Google have an obsession with runtime complexity? You haven’t asked me the time or space complexity for this problem. What gives?” You might also ask “Hang on, isn’t there a ‘Strong Hire’ rating you can give? How do we earn that?” Very good questions, both. This leads us to our final extra credit round…

Part 4: Can You Do Any Better?

At this point, I like to congratulate the candidate on a well-answered question and make it clear everything from here on out is extra credit. With that pressure gone, we can start to get creative.

So what is the runtime complexity of the BFS solution? In the worst case, we have to consider every single node and edge, making for a complexity of O(N+E), so effectively linear. That’s on top of the O(N+E) complexity of building the graph in the first place. For the purposes of a search engine, this is probably fine: a thousand units is enough for most reasonable applications, and performing a search in memory on each request isn’t an excessive burden.

However, we can do better. To motivate the question, consider what would happen if this code were inserted into a search engine. Some uncommon unit conversions are simply less uncommon than others, and so we’ll be computing them over and over again. Every time we do that, we’ll be performing a search, computing intermediate values, etc.

The first approach I often saw was to simply cache the results of a computation. Whenever a unit conversion is computed, we can always just add an edge between the two conversions. As a bonus, we would get the inverse conversion as well for free! Solved, right?

Indeed, this would give us an asymptotically constant lookup time, but it would come at the cost of storing the additional edges. This actually becomes quite expensive: over time we would tend toward a complete graph, as all pairs of conversions gradually become computed and stored. The number of edges possible in a graph grows with half the square of the number of nodes, so for a thousand nodes we’d need half a million edges. For ten thousand nodes we’d need around fifty million, etc.

Moving beyond the search engine problem, for a graph of a million nodes, we’d gradually tend toward half a trillion edges. That’s simply not reasonable to store, plus we’d waste time inserting things into the graph. We have to do better.

Fortunately, there’s a way to achieve constant-time conversion lookups without incurring quadratic space requirements. In fact, most of what it takes is already right under our noses.

Part 4: Constant Time

So it turns out that the “cache everything” solution is actually not far off from the mark. In that approach, we (eventually) end up with an edge between each node and every other node, meaning our conversion happen in a single edge lookup. But do we really need to store conversion from every node to every node? What if we just stored the conversion rates from one node to every other node?

Let’s take another look at that BFS solution:

from collections import deque

def bfs(rate_graph, start, end):
    to_visit = deque()
    to_visit.appendleft( (start, 1.0) )
    visited = set()

    while to_visit:
        node, rate_from_origin = to_visit.pop()
        if node == end:
            return rate_from_origin
        visited.add(node)
        for unit, rate in rate_graph.get_neighbors(node):
            if unit not in visited:
                to_visit.appendleft((unit, rate_from_origin * rate))

    return None

Let’s consider what’s happening here: we start with the origin node, and for every node we encounter, we compute the conversion rate from the origin to that node. Then, once we arrive at the destination, we return the rate between the origin and the destination, and we throw away the intermediate conversion rates.

Those intermediate rates are the key here. What if we don’t throw them away? What if instead we record them? All the most complex and obscure lookups become simple: to find the rate from A to B, first find the rate from X to B, then divide it by the rate from X to A, and you’re done! Visually it looks like this:

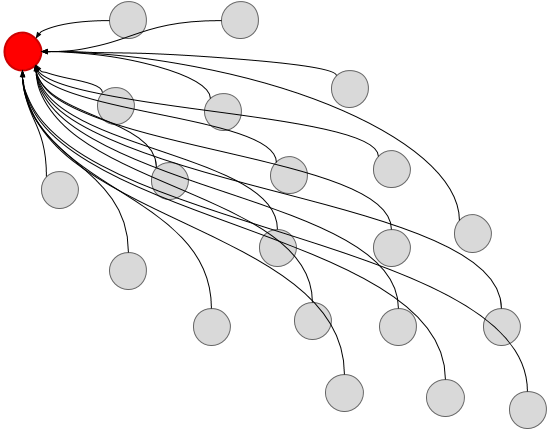
If we look at the code, it turns out we barely have to modify the BFS solution to compute this table:

from collections import deque

def make_conversions(graph):
    def conversions_bfs(rate_graph, start, conversions):
        to_visit = deque()
        to_visit.appendleft( (start, 1.0) )

        while to_visit:
            node, rate_from_origin = to_visit.pop()
            conversions[node] = (start, rate_from_origin)
            for unit, rate in rate_graph.get_neighbors(node):
                if unit not in conversions:
                    to_visit.append((unit, rate_from_origin * rate))

        return conversions

    conversions = {}
    for node in graph.get_nodes():
        if node not in conversions:
            conversions_bfs(graph, node, conversions)
    return conversions

The conversions structure is represented by a dict from a unit A to two values: the root for unit A’s connected component, and the conversion rate between the root unit and unit A. Since we insert a unit into this dict on each visitation, we can use the key space of this dict as the visited set instead of using a dedicated visitation set. Note also we don’t have an end node, and instead we iterate over nodes until we run out.

Outside this BFS, we have a helper function which iterates over the nodes in the graph. Whenever it encounters a node that isn’t in the conversions dict, it triggers a BFS starting at that node. This way, we are guaranteed to collapse all nodes into their connected components.

When we need to convert between units, we simple use the conversions structure we just computed:

def convert(conversions, start, end):
    'Given a conversion structure, performs a constant-time conversion'
    try:
        start_root, start_rate = conversions[start]
        end_root, end_rate = conversions[end]
    except KeyError:
        return None

    if start_root != end_root:
        return None

    return end_rate / start_rate

We handle the “no such unit” case by listening for an exception when accessing the conversions structure. We handle the “no such conversions” case by comparing the roots of the two quantities: if they don’t have the same root, they were encountered through two different BFS calls, meaning they are in two different connected components, and so no path between them exists. Finally we perform the conversion.

That’s it! We’ve now produced a solution that requires O(V+E) preprocessing (no worse than the earlier solutions) but also supports a constant time lookup. In theory, we are doubling the space requirements, but most of the time we no longer need to original graph, so we can simply delete it and use just this one. That being said, the space complexity is actually smaller than the original graph: the graph requires O(V+E) because it has to store all the edges as well as the vertices, whereas this structure only requires O(V), because we no longer need the edges.

Results

If you’ve made it this far, you might recall part of my aim was to test whether an easier problem could be still be useful in selecting worthwhile candidates and whether such a problem could give me a better picture of candidates’ abilities. I’d like to give you some definitive scientific answer, but at the end of the day all I have are anecdotes. However, I did notice some positive results.

If we break solving this problem into four hurdles (framing discussion, algorithm choice, implementation, constant time discussion), almost all candidates made it as far as “algorithm choice” by the end of the interview. As I suspected, the framing discussion turned out to be a good separator: candidates either got it immediately or struggled to grasp it despite substantial hints.

Right away, this is a useful signal. I can understand not knowing advanced or obscure data structures, because let’s be honest, how often are you going to have to implement a disjoint set. Graphs, however, are a fundamental data structure and are taught in just about every introductory level course on the topic. If a candidate struggles to understand them or can’t apply them readily, they are likely going to have a hard time thriving at Google (at least Google circa my employment there, I have no information about the Google of today).

Algorithm choice, on the other hand, turned out not to be a particularly useful source of signal. People who got over the framing stage usually arrived at using this algorithm without much trouble. I suspect this comes from the fact that search algorithms are almost always taught alongside graphs themselves, so if someone is familiar with one they’re likely to know the other.

Implementation turned out to be tricky. Many people had no problems implementing DFS recursively, but as I mentioned above, that implementation is not going to cut it in a production setting. To my surprise, the iterative BFS and DFS implementations do not seem to be at the tips of peoples’ fingers, and I often found that even after I gave substantial hints, people often faltered.

In my mind, since making it all the way through to the implementation stage earned a “Hire” from me, the “constant time discussion” stage was extra credit in my mind. While I went into detail in this post, I found it was usually more productive to have a verbal discussion instead of expecting code. Very few candidates got this one immediately. I often had to give substantial hints to lead people to this solution, and even then many people didn’t grasp it. Which is fine, the “Strong Hire” rating is supposed to be hard to achieve.

But Wait, There’s More!

That’s most of this problem, but if you’re interested in exploring this problem further, there’s a whole host of extensions I won’t be diving into. I leave the following as exercises for the reader:

First, a warm-up: in the constant time solution I laid out, I chose the root node of each connected component arbitrarily. In particular, I use the first node of that component we encounter. This is not optimal, because for all we know we’ve chosen some node way off on the fringes of the graph, while some other node might be more central and so have shorter paths to all other nodes. Your assignment is to replace this arbitrary choice with one which minimizes the number of multiplications required and this the floating point error propagation.

Second, this whole discussion assumes all equal-length paths through the graph are created equal, which isn’t always the case. One interesting variant of this problem is currency conversions: nodes are currencies, and edges from A to B and vice-versa are the bid/ask prices of each currency pair. We can rephrase the unit conversion question as a forex arbitrage question: implement an algorithm that, given a currency conversion graph, computes a cycle through the graph that can leave a trader with more money than when they started. Assume no transaction fees.

Finally, a real doozie: some units are expressed as a combination of various basic units. For instance, the watt is defined, in SI units, as “kilogram meters squared by seconds cubed”. The final challenge is to extend this system to support converting between these units given only the definitions of the basic SI units.

If you have questions, feel free to PM me on reddit.

Conclusion

When I chose to start using this problem, I hoped it would be a little easier than the ones I had asked before. I found my experiment was largely a success: people who did well on it generally aced it immediately, leaving us with plenty of time to talk about the advanced constant time solution. People who struggled tended to struggle in places other than the algorithmic conceptual leap: they couldn’t quite frame the problem in a useful way, or they sketched out a good solution but were unable to translate it into working code. Regardless of whether and where they struggled, I found I was able to give meaningful information about candidates’ strengths and weaknesses.

For your part, I hope you found this post useful. I realize it might not be as much of an algorithmic roller coaster as some of my previous editions, but the truth is that for all the algorithm-heavy reputation software interviewing has acquired, there’s a lot of complexity even in using a simple, well-known method. If you’d like to see code, take a look at this series’ github repo for more.

My next post will take a different angle. Switching from engineering to management has allowed me to experience the hiring process from a completely different point of view. I’m going to share my thoughts on how companies like Google and Reddit hire, and hopefully shed some light on the mysteries of the hiring process. If this sounds up your alley, make sure to follow me on Twitter or join the newsletter to be notified once it comes out. You can also join our discord to ask questions and discuss with others.